扭转弹簧力矩计算公式_扭转弹簧受力分析

1.发条弹簧厂家哪家好？知名发条弹簧厂家推荐

2.高一物理关于万有引力公式的理解及用法。请教。

3.简明材料力学的简明材料力学(第2版)

可利用平行轴定理，先测定物体绕与特定轴平行的过物体质心的轴的转动惯量J'，仪器可用扭摆或三线摆，若特定轴与过质心轴的距离为L，则物体绕特定轴转动的转动惯量J=J'+mL^2。

转动惯量在旋转动力学中的角色相当于线性动力学中的质量，可形式地理解为一个物体对于旋转运动的惯性，用于建立角动量、角速度、力矩和角加速度等数个量之间的关系。

扩展资料：

面积对于一轴的转动惯量，等于该面积对于同此轴平行并通过形心之轴的转动惯量加上该面积同两轴间距离平方的乘积。由于和式的第二项恒大于零，因此面积绕过形心之轴的转动惯量是绕该束平行轴诸转动惯量中的最小者。

转动惯量只决定于刚体的形状、质量分布和转轴的位置，而同刚体绕轴的转动状态（如角速度的大小）无关。形状规则的匀质刚体，其转动惯量可直接用公式计算得到。

而对于不规则刚体或非均质刚体的转动惯量，一般通过实验的方法来进行测定，因而实验方法就显得十分重要。转动惯量应用于刚体各种运动的动力学计算中。

百度百科--转动惯量

发条弹簧厂家哪家好？知名发条弹簧厂家推荐

因为机械钟摆的悬挂处是固定的并且很光滑，而用手提着绳子，手是不稳定的，这样会消耗掉重物摆动时的惯性，而且钟摆的悬挂处的接触面也十分小，这就大大的减小的磨擦的阻力，加上摆臂是有一定的硬度的，而不像绳子是软体，这样可以减少摆动过程中的能量损耗，所以以靠惯性钟摆可以摆动好久

高一物理关于万有引力公式的理解及用法。请教。

发条弹簧，又被称为卷弹簧，是将材料绕制成平面为螺旋形的一种弹簧制品，是众多五金制品中的其中一种，主要运用于钟表、记录仪器、机动玩具等方面。发条弹簧是利用弹性来工作，一般是由发条弹簧钢制成，用以控制机件的运动、缓和冲击或震动、贮蓄能量等。优质的弹簧材料，具有较好的热稳定性、抗松弛、抗氧化能力、腐蚀能力。下面，小编为大家介绍三家发条弹簧的厂家。

东莞市永晟金属制品有限公司

永晟金属制品有限公司是一家专业生产和销售金属制品的公司，公司坚持诚信经营、顾客至上的理念，有丰富的生产研发经验和核心技术，提供优质的售前和售后服务，全方位满足顾客的需求。公司主营的产品有发条弹簧、卷簧、涡卷弹簧、不锈钢发条等等。公司地址位于广东省东莞市桥头镇禾坑村禾石路第二工业区27号C栋三楼B区。

深圳市东际弹簧有限公司

东际弹簧有限公司是一家致力于生产和加工各种弹簧产品的公司，公司拥有先进的生产设备和专业的技术人才，对产品不断改良和创新。公司生产的产品种类齐全、质量上乘、价格合理，获得广大消费者的喜爱和支持。公司主营的产品有发条弹簧、涡卷弹簧、不锈钢发条、恒力发条、吸尘器发条、收线发条、电器发条、玩具发条、碳刷发条、窗帘发条等等。公司的地址是广东省深圳市宝安区西乡街道办固戍社区朱坳工业园B栋4楼之01。

东莞市协励五金有限公司

协励五金有限公司是一家集精密五金产品研发、生产、加工和销售与一体的公司，公司拥有专业的开发和管理团队，以及科学的质量管理体系，对产品进行层层的质量把关，致力于打造质量一流的产品。公司主营的产品包括发条弹簧、弹片、油封弹簧、金属线类成型等等。公司的地址位于广东省东莞市大岭山镇杨屋村第四工业区430号。

发条弹簧特点

发条弹簧又称作卷弹簧。螺旋线在一个平面内的弹簧，弹簧是将材料绕制成平面螺旋形的一种弹簧，弹簧一端固定，另一端作用扭矩后材料材料受弯曲力矩，产生弯曲弹性变形，因而弹簧在自身平面产生扭转。其变形角的大小和扭矩成正比，具有高扭力，与多角度之扭转力距故运用于长时间作功之机构，具有不易疲劳之特性，其运用类似扭簧。

发条弹簧应用：

运用类别大致应用钟表、记录仪器、机动玩具、卷尺、汽车起动马达、收纳线盒等。

发条弹簧分类：

平面涡卷弹簧按与相邻工作部件是否接触分类：①非接触型平面涡卷弹簧，②接触型平面涡卷弹簧。?平面涡卷弹簧固定端的固定方式有：①铰式固定，②销式固定，③v形固定，④衬片固定。

发条弹簧材质：

发条弹簧一般选用55Si2Mn、60Si2MnA、55SiMnVB、55SiMnMoV、60CrMn、60CrMnB、302、316等牌号的扁钢带。

发条弹簧是用细长弹簧材料，绕制成平面螺旋线形的弹簧。弹簧一端固定，另一端作用扭矩后，材料受弯曲力矩，产生弯曲弹性变形，因而弹簧在自身平面内产生扭转。其变形角的大小与扭矩成正比

发条弹簧的卷绕成形比较简单，它的刚度较小，一般在静载荷下工作。由于卷绕圈数可以很多，变形角大，具有在较小体积内储存较多的能量的特点。材料载面形状可以是长方形的单体积储存能能力较大，用得较多

平面发条弹簧根据相邻各圈接触与否，分为非触形和接触形两类。它们的用途，特性和设计计算方法都有所不同

非接触形发条弹簧在工作中各圈均不接触，常用来生产反作用力矩。例如用于电动机电刷的压紧弹簧和仪器、钟表中的游丝等均属于这一类

接触形发条弹簧的相邻各互相接触，圈数较多，可储存较大的能量，常用来作为各种仪器或钟表机构中的原动机

　以上，就是小编为大家提供的发条弹簧生产厂家的相关信息。发条弹簧按照其形状区分分，可以分为螺旋发条弹簧、平面发条弹簧、发条弹簧、板发条弹簧等。大家可以根据自己的需要，经过货比三家后，向厂家进行详尽的咨询再进行订购。市面上有弹簧扭转试验机，可以通过这种试验机测试各种发条弹簧的扭转角、扭转力矩等技术参数。

土巴兔在线免费为大家提供“各家装修报价、1-4家本地装修公司、3套装修设计方案”，还有装修避坑攻略！点击此链接：s://.to8to/yezhu/zxbj-cszy.php?to8to_from=seo_zhidao_m_jiare&wb，就能免费领取哦~

简明材料力学的简明材料力学(第2版)

一、质点的运动（1）------直线运动

1）匀变速直线运动

1.平均速度V平＝s/t（定义式） 2.有用推论Vt2-Vo2＝2as

3.中间时刻速度Vt/2＝V平＝(Vt+Vo)/2 4.末速度Vt＝Vo+at

5.中间位置速度Vs/2＝[(Vo2+Vt2)/2]1/2 6.位移s＝V平t＝Vot+at2/2＝Vt/2t

7.加速度a＝(Vt-Vo)/t ｛以Vo为正方向，a与Vo同向(加速)a>0；反向则a<0｝

8.实验用推论Δs＝aT2 ｛Δs为连续相邻相等时间(T)内位移之差｝

9.主要物理量及单位:初速度(Vo):m/s；加速度(a):m/s2；末速度(Vt):m/s；时间(t)秒(s)；位移(s):米（m）；路程:米；速度单位换算：1m/s=3.6km/h。

注：

(1)平均速度是矢量;

(2)物体速度大,加速度不一定大;

(3)a=(Vt-Vo)/t只是量度式，不是决定式;

(4)其它相关内容：质点、位移和路程、参考系、时间与时刻〔见第一册P19〕/s--t图、v--t图/速度与速率、瞬时速度〔见第一册P24〕。

2)自由落体运动

1.初速度Vo＝0 2.末速度Vt＝gt

3.下落高度h＝gt2/2（从Vo位置向下计算） 4.推论Vt2＝2gh

注:

(1)自由落体运动是初速度为零的匀加速直线运动，遵循匀变速直线运动规律；

(2)a＝g＝9.8m/s2≈10m/s2（重力加速度在赤道附近较小,在高山处比平地小，方向竖直向下）。

（3)竖直上抛运动

1.位移s＝Vot-gt2/2 2.末速度Vt＝Vo-gt （g=9.8m/s2≈10m/s2）

3.有用推论Vt2-Vo2＝-2gs 4.上升最大高度Hm＝Vo2/2g(抛出点算起）

5.往返时间t＝2Vo/g （从抛出落回原位置的时间）

注:

(1)全过程处理:是匀减速直线运动，以向上为正方向，加速度取负值；

(2)分段处理：向上为匀减速直线运动，向下为自由落体运动，具有对称性；

(3)上升与下落过程具有对称性,如在同点速度等值反向等。

二、质点的运动（2）----曲线运动、万有引力

1)平抛运动

1.水平方向速度：Vx＝Vo 2.竖直方向速度：Vy＝gt

3.水平方向位移：x＝Vot 4.竖直方向位移：y＝gt2/2

5.运动时间t＝(2y/g）1/2(通常又表示为(2h/g)1/2)

6.合速度Vt＝(Vx2+Vy2)1/2＝[Vo2+(gt)2]1/2

合速度方向与水平夹角β:tgβ＝Vy/Vx＝gt/V0

7.合位移：s＝(x2+y2)1/2,

位移方向与水平夹角α:tgα＝y/x＝gt/2Vo

8.水平方向加速度：ax=0；竖直方向加速度：ay＝g注：

(1)平抛运动是匀变速曲线运动，加速度为g，通常可看作是水平方向的匀速直线运与竖直方向的自由落体运动的合成；

(2)运动时间由下落高度h(y)决定与水平抛出速度无关；

（3）θ与β的关系为tgβ＝2tgα；

（4）在平抛运动中时间t是解题关键；(5)做曲线运动的物体必有加速度，当速度方向与所受合力(加速度)方向不在同一直线上时，物体做曲线运动。

2）匀速圆周运动

1.线速度V＝s/t＝2πr/T 2.角速度ω＝Φ/t＝2π/T＝2πf

3.向心加速度a＝V2/r＝ω2r＝(2π/T)2r 4.向心力F心＝mV2/r＝mω2r＝mr(2π/T)2＝mωv=F合

5.周期与频率：T＝1/f 6.角速度与线速度的关系：V＝ωr

7.角速度与转速的关系ω＝2πn(此处频率与转速意义相同)

8.主要物理量及单位：弧长(s):米(m)；角度(Φ)：弧度（rad）；频率（f）：赫（Hz）；周期（T）：秒（s）；转速（n）：r/s；半径(r):米（m）；线速度（V）：m/s；角速度（ω）：rad/s；向心加速度：m/s2。

注：

（1）向心力可以由某个具体力提供，也可以由合力提供，还可以由分力提供，方向始终与速度方向垂直，指向圆心；

（2）做匀速圆周运动的物体，其向心力等于合力，并且向心力只改变速度的方向，不改变速度的大小，因此物体的动能保持不变，向心力不做功，但动量不断改变。

3)万有引力

1.开普勒第三定律：T2/R3＝K(＝4π2/GM)｛R:轨道半径，T:周期，K:常量(与行星质量无关，取决于中心天体的质量)｝

2.万有引力定律：F＝Gm1m2/r2 （G＝6.67×10-11N?m2/kg2，方向在它们的连线上）

3.天体上的重力和重力加速度：GMm/R2＝mg；g＝GM/R2 ｛R:天体半径(m)，M：天体质量（kg）｝

4.卫星绕行速度、角速度、周期：V＝(GM/r)1/2；ω＝(GM/r3)1/2；T＝2π(r3/GM)1/2｛M：中心天体质量｝

5.第一(二、三)宇宙速度V1＝(g地r地)1/2＝(GM/r地)1/2＝7.9km/s；V2＝11.2km/s；V3＝16.7km/s

6.地球同步卫星GMm/(r地+h)2＝m4π2(r地+h)/T2｛h≈36000km，h:距地球表面的高度，r地:地球的半径｝

注:

(1)天体运动所需的向心力由万有引力提供,F向＝F万；

(2)应用万有引力定律可估算天体的质量密度等；

(3)地球同步卫星只能运行于赤道上空，运行周期和地球自转周期相同；

(4)卫星轨道半径变小时,势能变小、动能变大、速度变大、周期变小（一同三反）；

(5)地球卫星的最大环绕速度和最小发射速度均为7.9km/s。

三、力（常见的力、力的合成与分解）

1）常见的力

1.重力G＝mg （方向竖直向下，g＝9.8m/s2≈10m/s2，作用点在重心，适用于地球表面附近）

2.胡克定律F＝kx ｛方向沿恢复形变方向，k：劲度系数(N/m)，x：形变量(m)｝

3.滑动摩擦力F＝μFN ｛与物体相对运动方向相反，μ：摩擦因数，FN：正压力(N)｝

4.静摩擦力0≤f静≤fm （与物体相对运动趋势方向相反，fm为最大静摩擦力）

5.万有引力F＝Gm1m2/r2 （G＝6.67×10-11N?m2/kg2,方向在它们的连线上）

6.静电力F＝kQ1Q2/r2 （k＝9.0×109N?m2/C2,方向在它们的连线上）

7.电场力F＝Eq （E：场强N/C，q：电量C，正电荷受的电场力与场强方向相同）

8.安培力F＝BILsinθ （θ为B与L的夹角，当L⊥B时:F＝BIL，B//L时:F＝0）

9.洛仑兹力f＝qVBsinθ （θ为B与V的夹角，当V⊥B时：f＝qVB，V//B时:f＝0）注:

(1)劲度系数k由弹簧自身决定;

(2)摩擦因数μ与压力大小及接触面积大小无关，由接触面材料特性与表面状况等决定;

(3)fm略大于μFN，一般视为fm≈μFN;

(4)其它相关内容：静摩擦力（大小、方向）〔见第一册P8〕；

(5)物理量符号及单位B：磁感强度(T)，L：有效长度(m)，I:电流强度(A)，V：带电粒子速度(m/s),q:带电粒子（带电体）电量(C);

(6)安培力与洛仑兹力方向均用左手定则判定。

2）力的合成与分解

1.同一直线上力的合成同向:F＝F1+F2， 反向：F＝F1-F2 (F1>F2)

2.互成角度力的合成：

F＝(F12+F22+2F1F2cosα)1/2（余弦定理） F1⊥F2时:F＝(F12+F22)1/2

3.合力大小范围：|F1-F2|≤F≤|F1+F2|

4.力的正交分解：Fx＝Fcosβ，Fy＝Fsinβ（β为合力与x轴之间的夹角tgβ＝Fy/Fx）

注：

(1)力(矢量)的合成与分解遵循平行四边形定则;

（2）合力与分力的关系是等效替代关系,可用合力替代分力的共同作用,反之也成立;

(3)除公式法外，也可用作图法求解,此时要选择标度,严格作图;

(4)F1与F2的值一定时,F1与F2的夹角(α角)越大，合力越小;

（5）同一直线上力的合成，可沿直线取正方向，用正负号表示力的方向，化简为代数运算。四、动力学（运动和力）

1.牛顿第一运动定律(惯性定律）：物体具有惯性，总保持匀速直线运动状态或静止状态,直到有外力迫使它改变这种状态为止

2.牛顿第二运动定律：F合＝ma或a＝F合/ma{由合外力决定,与合外力方向一致}

3.牛顿第三运动定律：F＝-F?{负号表示方向相反,F、F?各自作用在对方，平衡力与作用力反作用力区别，实际应用：反冲运动}

4.共点力的平衡F合＝0，推广 ｛正交分解法、三力汇交原理｝

5.超重：FN>G，失重：FN<G {加速度方向向下，均失重，加速度方向向上，均超重}

6.牛顿运动定律的适用条件：适用于解决低速运动问题，适用于宏观物体，不适用于处理高速问题，不适用于微观粒子〔见第一册P67〕

注:平衡状态是指物体处于静止或匀速直线状态,或者是匀速转动。

五、振动和波（机械振动与机械振动的传播）

1.简谐振动F＝-kx {F:回复力，k:比例系数，x:位移，负号表示F的方向与x始终反向}

2.单摆周期T＝2π(l/g)1/2 ｛l:摆长(m)，g:当地重力加速度值，成立条件:摆角θ<100;l>>r｝

3.受迫振动频率特点：f＝f驱动力

4.发生共振条件:f驱动力＝f固，A＝max，共振的防止和应用〔见第一册P175〕

5.机械波、横波、纵波〔见第二册P2〕

6.波速v＝s/t＝λf＝λ/T{波传播过程中，一个周期向前传播一个波长；波速大小由介质本身所决定}

7.声波的波速(在空气中）0℃：332m/s；20℃:344m/s；30℃:349m/s；(声波是纵波)

8.波发生明显衍射（波绕过障碍物或孔继续传播）条件：障碍物或孔的尺寸比波长小，或者相差不大

9.波的干涉条件：两列波频率相同(相差恒定、振幅相近、振动方向相同)

10.多普勒效应:由于波源与观测者间的相互运动，导致波源发射频率与接收频率不同｛相互接近，接收频率增大，反之，减小〔见第二册P21〕｝

注：

（1）物体的固有频率与振幅、驱动力频率无关，取决于振动系统本身；

（2）加强区是波峰与波峰或波谷与波谷相遇处，减弱区则是波峰与波谷相遇处；

（3）波只是传播了振动，介质本身不随波发生迁移,是传递能量的一种方式；

（4）干涉与衍射是波特有的；

(5)振动图象与波动图象；

(6)其它相关内容：超声波及其应用〔见第二册P22〕/振动中的能量转化〔见第一册P173〕。

六、冲量与动量(物体的受力与动量的变化）

1.动量：p＝mv ｛p:动量(kg/s)，m:质量(kg)，v:速度(m/s)，方向与速度方向相同｝

3.冲量：I＝Ft ｛I:冲量(N?s)，F:恒力(N)，t:力的作用时间(s)，方向由F决定｝

4.动量定理：I＝Δp或Ft＝mvt–mvo {Δp:动量变化Δp＝mvt–mvo，是矢量式}

5.动量守恒定律：p前总＝p后总或p＝p’?也可以是m1v1+m2v2＝m1v1?+m2v2?

6.弹性碰撞：Δp＝0；ΔEk＝0 {即系统的动量和动能均守恒}

7.非弹性碰撞Δp＝0；0<ΔEK<ΔEKm {ΔEK：损失的动能，EKm：损失的最大动能}

8.完全非弹性碰撞Δp＝0；ΔEK＝ΔEKm {碰后连在一起成一整体}

9.物体m1以v1初速度与静止的物体m2发生弹性正碰:

v1?＝(m1-m2)v1/(m1+m2) v2?＝2m1v1/(m1+m2)

10.由9得的推论-----等质量弹性正碰时二者交换速度(动能守恒、动量守恒)

11.m水平速度vo射入静止置于水平光滑地面的长木块M，并嵌入其中一起运动时的机械能损失

E损=mvo2/2-(M+m)vt2/2＝fs相对 {vt:共同速度，f:阻力，s相对相对长木块的位移}

注：

(1)正碰又叫对心碰撞，速度方向在它们“中心”的连线上;

(2)以上表达式除动能外均为矢量运算,在一维情况下可取正方向化为代数运算;

（3）系统动量守恒的条件:合外力为零或系统不受外力，则系统动量守恒（碰撞问题、爆炸问题、反冲问题等）;

(4)碰撞过程(时间极短，发生碰撞的物体构成的系统)视为动量守恒,原子核衰变时动量守恒;

(5)爆炸过程视为动量守恒，这时化学能转化为动能，动能增加；(6)其它相关内容：反冲运动、火箭、航天技术的发展和宇宙航行〔见第一册P128〕。

作/译者：刘鸿文

出版社：高等教育出版社

出版日期：2008年01月

ISBN：87040239287 [十位:7040239280]

页数：341

重约：0.424KG

定价：￥27.50 本教材是普通高等教育“十一五”国家级规划教材。它保持了原书的风格和特色,作了少量的修订。全书精选的材料力学的基本内容,与第一版相同,包括第1章至第13章,计有:绪论,拉伸、压缩与剪切,扭转,平面图形的几何性质,弯曲内力,弯曲应力,弯曲变形,应力状态分析和强度理论,组合变形,压杆稳定,动载荷,交变应力,能量方法和超静定结构。《简明材料力学》如不讲授最后一章,并对其他章节作适当删减,可用作少学时的材料力学课程的教材;若能在能量方法、超静定结构等方面略作补充,《简明材料力学》亦可用作多学时材料力学课程的教材。

刘鸿文主编的《材料力学实验》(第3版)可与《简明材料力学》配套使用。

与刘鸿文主编的《材料力学》(第4版)配套的、由高等教育出版社出版的《材料力学学习指导书》,也可供使用本教材的学生复习、解题及教师备课时使用。 第1章 绪论

1.1 材料力学的任务

1.2 变形固体的基本设

1.3 内力、应力和截面法

1.4 位移、变形与应变

1.5 杆件变形的基本形式

习题

第2章 拉伸、压缩与剪切

2.1 轴向拉伸与压缩的概念和实例

2.2 拉伸或压缩时杆横截面上的内力和应力

2.3 材料拉伸时的力学性能

2.4 材料压缩时的力学性能

2.5 失效、安全因数和强度计算

2.6 杆件轴向拉伸或压缩时的变形

2.7 轴向拉伸或压缩的应变能

2.8 拉伸、压缩超静定问题

2.9 温度应力和装配应力

2.10应力集中的概念

2.11剪切和挤压的实用计算

习题

第3章 扭转

3.1 扭转的概念和实例

3.2 外力偶矩的计算扭矩和扭矩图

3.3 纯剪切

3.4 圆轴扭转时的应力

3.5 圆轴扭转时的变形

3.6 扭转应变能

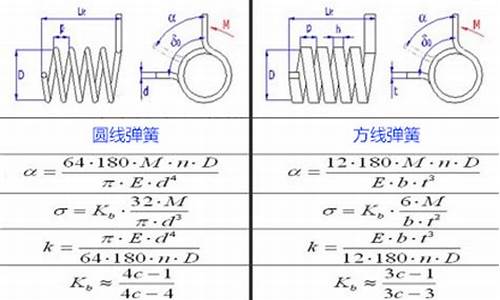
3.7 圆柱形密圈螺旋弹簧

3.8 矩形截面杆扭转理论简介

习题

第4章 平面图形的几何性质

4.1 静矩和形心

4.2 惯性矩和惯性半径

4.3 惯性积

4.4 平行移轴公式

4.5 转轴公式主惯性轴

习题

第5章 弯曲内力

5.1 弯曲的概念和实例

5.2 梁的支座和载荷的简化

5.3 剪力和弯矩

5.4 剪力方程和弯矩方程剪力图和弯矩图

5.5 载荷集度、剪力和弯矩间的关系

5.6 刚架和曲杆的弯曲内力

习题

第6章 弯曲应力

6.1 梁的纯弯曲

6.2 纯弯曲时的正应力

6.3 横力弯曲时的正应力

6.4 弯曲切应力

6.5 提高弯曲强度的措施

习题

第7章 弯曲变形

7.1 工程问题中的弯曲变形挠度和转角

7.2 挠曲线的近似微分方程

7.3 用积分法求弯曲变形

7.4 用叠加法求弯曲变形

7.5 弯曲应变能

7.6 简单超静定梁

7.7 提高梁弯曲刚度的措施

习题

第8章 应力状态分析和强度理论

8.1 应力状态概述单向拉伸时斜截面上的应力.

8.2 二向和三向应力状态的实例

8.3 二向应力状态分析

8.4 二向应力状态的应力圆

8.5 三向应力状态简介

8.6 广义胡克定律

8.7 复杂应力状态下的应变能密度

8.8 强度理论概述

8.9 四种常用强度理论

习题

第9章 组合变形

9.1 组合变形和叠加原理

9.2 拉伸或压缩与弯曲的组合

9.3 斜弯曲

9.4 扭转与弯曲的组合

习题

第10章 压杆稳定

10.1 压杆稳定的概念

10.2 两端铰支细长压杆的临界压力

10.3 其他支座条件下细长压杆的临界压力

10.4 欧拉公式的适用范围经验公式

10.5 压杆的稳定校核

10.6 提高压杆稳定性的措施

习题

第11章 动载荷

11.1 概述

11.2 动静法的应用

11.3 受冲击杆件的应力和变形

习题

第12章 交变应力

12.1 交变应力与疲劳失效

12.2 循环特征、平均应力和应力幅

12.3 持久极限

12.4 影响持久极限的因素

12.5 对称循环下的疲劳强度计算

12.6 不对称循环下和扭弯组合下的疲劳强度计算

12.7 提高构件疲劳强度的措施

习题

第13章 能量方法和超静定结构

13.1 应变能的计算

13.2 互等定理

13.3 卡氏定理

13.4 莫尔定理

13.5 用力法解超静定结构

习题

附录A 型钢表

附录B 习题答案

参考文献

作者简介