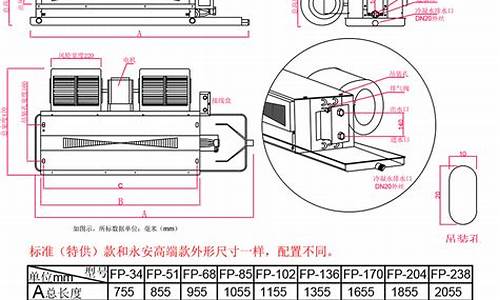
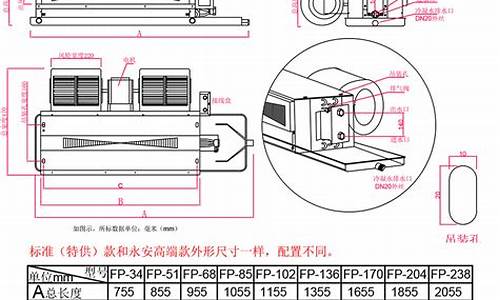
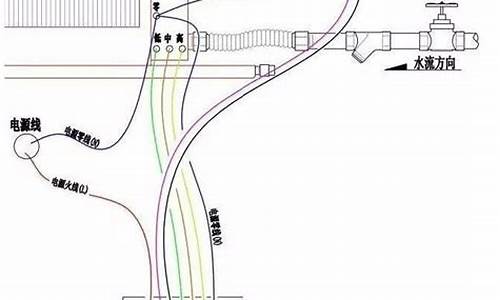
扭转弹簧力矩计算公式图解_扭转弹簧力矩计算公式

1.如何用扭摆法测定任意形状物体绕特定轴转动的转动惯量？

作/译者：刘鸿文

出版社：高等教育出版社

出版日期：2008年01月

ISBN：87040239287 [十位:7040239280]

页数：341

重约：0.424KG

定价：￥27.50 本教材是普通高等教育“十一五”国家级规划教材。它保持了原书的风格和特色,作了少量的修订。全书精选的材料力学的基本内容,与第一版相同,包括第1章至第13章,计有:绪论,拉伸、压缩与剪切,扭转,平面图形的几何性质,弯曲内力,弯曲应力,弯曲变形,应力状态分析和强度理论,组合变形,压杆稳定,动载荷,交变应力,能量方法和超静定结构。《简明材料力学》如不讲授最后一章,并对其他章节作适当删减,可用作少学时的材料力学课程的教材;若能在能量方法、超静定结构等方面略作补充,《简明材料力学》亦可用作多学时材料力学课程的教材。

刘鸿文主编的《材料力学实验》(第3版)可与《简明材料力学》配套使用。

与刘鸿文主编的《材料力学》(第4版)配套的、由高等教育出版社出版的《材料力学学习指导书》,也可供使用本教材的学生复习、解题及教师备课时使用。 第1章 绪论

1.1 材料力学的任务

1.2 变形固体的基本设

1.3 内力、应力和截面法

1.4 位移、变形与应变

1.5 杆件变形的基本形式

习题

第2章 拉伸、压缩与剪切

2.1 轴向拉伸与压缩的概念和实例

2.2 拉伸或压缩时杆横截面上的内力和应力

2.3 材料拉伸时的力学性能

2.4 材料压缩时的力学性能

2.5 失效、安全因数和强度计算

2.6 杆件轴向拉伸或压缩时的变形

2.7 轴向拉伸或压缩的应变能

2.8 拉伸、压缩超静定问题

2.9 温度应力和装配应力

2.10应力集中的概念

2.11剪切和挤压的实用计算

习题

第3章 扭转

3.1 扭转的概念和实例

3.2 外力偶矩的计算扭矩和扭矩图

3.3 纯剪切

3.4 圆轴扭转时的应力

3.5 圆轴扭转时的变形

3.6 扭转应变能

3.7 圆柱形密圈螺旋弹簧

3.8 矩形截面杆扭转理论简介

习题

第4章 平面图形的几何性质

4.1 静矩和形心

4.2 惯性矩和惯性半径

4.3 惯性积

4.4 平行移轴公式

4.5 转轴公式主惯性轴

习题

第5章 弯曲内力

5.1 弯曲的概念和实例

5.2 梁的支座和载荷的简化

5.3 剪力和弯矩

5.4 剪力方程和弯矩方程剪力图和弯矩图

5.5 载荷集度、剪力和弯矩间的关系

5.6 刚架和曲杆的弯曲内力

习题

第6章 弯曲应力

6.1 梁的纯弯曲

6.2 纯弯曲时的正应力

6.3 横力弯曲时的正应力

6.4 弯曲切应力

6.5 提高弯曲强度的措施

习题

第7章 弯曲变形

7.1 工程问题中的弯曲变形挠度和转角

7.2 挠曲线的近似微分方程

7.3 用积分法求弯曲变形

7.4 用叠加法求弯曲变形

7.5 弯曲应变能

7.6 简单超静定梁

7.7 提高梁弯曲刚度的措施

习题

第8章 应力状态分析和强度理论

8.1 应力状态概述单向拉伸时斜截面上的应力.

8.2 二向和三向应力状态的实例

8.3 二向应力状态分析

8.4 二向应力状态的应力圆

8.5 三向应力状态简介

8.6 广义胡克定律

8.7 复杂应力状态下的应变能密度

8.8 强度理论概述

8.9 四种常用强度理论

习题

第9章 组合变形

9.1 组合变形和叠加原理

9.2 拉伸或压缩与弯曲的组合

9.3 斜弯曲

9.4 扭转与弯曲的组合

习题

第10章 压杆稳定

10.1 压杆稳定的概念

10.2 两端铰支细长压杆的临界压力

10.3 其他支座条件下细长压杆的临界压力

10.4 欧拉公式的适用范围经验公式

10.5 压杆的稳定校核

10.6 提高压杆稳定性的措施

习题

第11章 动载荷

11.1 概述

11.2 动静法的应用

11.3 受冲击杆件的应力和变形

习题

第12章 交变应力

12.1 交变应力与疲劳失效

12.2 循环特征、平均应力和应力幅

12.3 持久极限

12.4 影响持久极限的因素

12.5 对称循环下的疲劳强度计算

12.6 不对称循环下和扭弯组合下的疲劳强度计算

12.7 提高构件疲劳强度的措施

习题

第13章 能量方法和超静定结构

13.1 应变能的计算

13.2 互等定理

13.3 卡氏定理

13.4 莫尔定理

13.5 用力法解超静定结构

习题

附录A 型钢表

附录B 习题答案

参考文献

作者简介

如何用扭摆法测定任意形状物体绕特定轴转动的转动惯量？

就是磁场对通电线圈有安培力的作用.从而使得线圈发生偏转,同时线圈上的两个螺旋弹簧由于线圈偏转而产生一个阻碍线圈继续转动的力矩.当这俩个力矩(一个是安培力矩,一个是扭转力矩)相等时,线圈停止转动.

设线圈有N匝,流过电流为I,磁感应强度为B,线圈面积为S,弹簧的扭转系数为K,有:

NBIS=K*θ (θ表示弹簧扭转的角度,也就是线圈转动的角度)

很显然,I与θ成正比

可利用平行轴定理，先测定物体绕与特定轴平行的过物体质心的轴的转动惯量J'，仪器可用扭摆或三线摆，若特定轴与过质心轴的距离为L，则物体绕特定轴转动的转动惯量J=J'+mL^2。

转动惯量在旋转动力学中的角色相当于线性动力学中的质量，可形式地理解为一个物体对于旋转运动的惯性，用于建立角动量、角速度、力矩和角加速度等数个量之间的关系。

扩展资料：

面积对于一轴的转动惯量，等于该面积对于同此轴平行并通过形心之轴的转动惯量加上该面积同两轴间距离平方的乘积。由于和式的第二项恒大于零，因此面积绕过形心之轴的转动惯量是绕该束平行轴诸转动惯量中的最小者。

转动惯量只决定于刚体的形状、质量分布和转轴的位置，而同刚体绕轴的转动状态（如角速度的大小）无关。形状规则的匀质刚体，其转动惯量可直接用公式计算得到。

而对于不规则刚体或非均质刚体的转动惯量，一般通过实验的方法来进行测定，因而实验方法就显得十分重要。转动惯量应用于刚体各种运动的动力学计算中。

百度百科--转动惯量