扭转弹簧扭力计算_扭转弹簧力矩计算公式

1.怎样计算弹簧的力？

2.怎么计算门的推力及弹簧扭矩

3.大家知道常用的弹簧参数有哪些吗？

4.扭力弹簧可扭转角度与什么有关

5.1.4线径,扭簧转动1度多少扭矩

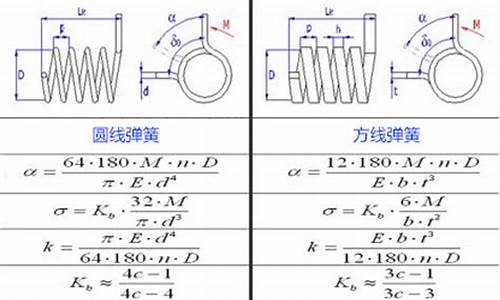
扭力弹簧（Torsion Spring）乃变体弹簧之极至，由单扭簧至双扭簧异形扭簧，乃至各种扭杆之变形，得依设计成型。

扭簧（Torsion Spring）为所有弹簧类别中设计原理较为复杂的一种，型式的变化亦相当活泼，故设计时所涉及的理论也最为繁琐。因此设计时亦较难掌握

扭簧之必要资料：

（1） 自由长度。

（2） 控制直径：(a)外径、(b)内径、(c)所套管之内径，或(d)所穿越圆杆之外径。

（3） 钢丝尺寸“线径”。

（4） 材料（种类及等级）。

（5）

（6） 扭转力：偏转至某一角度之磅数。

（7） 最大挠度（自由位置算起之角度）。

（8） 末端之形式。

请注明：材料直径(d)，外径(D)，扭臂长(L)，自由高度(Lo)，以及其它几何尺寸，如导矩（T 1 T 2…… T j ）和对应和对应扭转角度（Ψ ）

怎样计算弹簧的力？

弹簧的深度是指弹簧的伸缩程度。

弹簧是一种利用弹性来工作的机械零件。用弹性材料制成的零件在外力作用下发生形变，除去外力后又恢复原状。亦作“ 弹簧 ”。一般用弹簧钢制成。弹簧的种类复杂多样，按形状分，主要有螺旋弹簧、涡卷弹簧、板弹簧、异型弹簧等。

弹力公式：

F=kx，F为弹力，k为劲度系数（或倔强系数），x为弹簧拉长（或压短）的长度。

扭力弹簧：

扭力弹簧（扭簧）利用杠杆的原理，通过对材质柔软、韧度较大的弹性材料的扭曲或旋转，使之具有极大的机械能。是承受扭转变形的弹簧，它的工作部分也是各圈或是紧密围绕或是分开围绕。

扭转弹簧的端部结构是加工成各种形状的扭臂，由单扭至双扭，乃至各种扭杆之变形，得依设计成型。扭转弹簧常用于机械中的平衡机构，在汽车、机床、电器等工业生产中广泛应用。

以上内容参考：百度百科——弹簧

怎么计算门的推力及弹簧扭矩

F=f*G*d^4/(8*n*D^3)

F：压力，N

f：变形量，mm

G：材料的切变模量,MPa

d：钢丝直径，mm

n：弹簧有效圈数

D：弹簧中径，mm

关于G，一般碳素弹簧钢丝取79000。

你的问题没有谈及材质，希望仅仅是一个疏忽。

304,G=71000.

F=f*G*d^4/(8*n*D^3)

=(38-17)*71000*1.7^4/(8*38/5.5*10^3)

=225.3(N) =23kgf

大家知道常用的弹簧参数有哪些吗？

因为将它们两端平齐的套在一起后，下端挂一重物，平衡时两弹簧的弹力比为2：1.

所以劲度系数的比为2:1

将它们串连后再挂上原重物时力相同.

所以伸长量之比为1:2

://baike.baidu/view/38962.htm

形变

凡物体受到外力而发生形状变化谓之“形变”。物体由于外因或内在缺陷，物质微粒的相对位置发生改变，也可引起形态的变化。形变的种类有：

1.纵向形变：杆的两端受到压力或拉力时，长度发生改变；

2.体积形变：物体体积大小的改变；

3.切变：物体两相对的表面受到在表面内的（切向）力偶作用时，两表面发生相对位移，称为切变；

4.扭转：一圆柱状物体，两端各受方向相反的力矩作用而扭转，称扭转形变；

5.弯曲：两端固定的钢筋，因负荷而弯曲，称弯曲形变。

无论产生什么形变，都可归结为长变与切变。

参考资料：

://baike.baidu/view/38962.htm

扭力弹簧可扭转角度与什么有关

弹簧的基础常识，对于从事弹簧行业的人都是非常有用的知识，下面我们来介绍一下。弹簧各部分名称及尺寸关系：

1、谈弹簧丝直径d:制造弹簧的钢丝直径。

2、弹簧外径D:弹簧的最大外径。

3、弹簧内径D1：弹簧的最小外径。

4、弹簧中径D2：弹簧的平均直径。它们的计算公式为：D2＝（D＋D1）÷2＝D1＋d＝D－d。

5、支撑圈数n2：为了使弹簧在工作时受力均匀，保证轴线垂直端面、制造时，常将弹簧两端并紧。并紧的圈数仅起支撑作用，称为支撑圈。一般有1.5T、2T、2.5T，常用的是2T。

6、有效圈数n:弹簧能保持相同节距的圈数。

7、总圈数n1:有效圈数与支撑圈的和。即n1=n+n2。

8、自由高H0:弹簧在未受外力作用下的高度。由下式计算：H0=nt+(n2-0.5)d=nt+1.5d(n2=2时）。

9、螺旋方向：有左右旋之分，常用右旋，图纸没注明的一般用右旋。

弹簧的规定画法：

有效圈数在4圈以上的弹簧，可只画出其两端1～2圈（不含支撑圈）。中间用通过弹簧钢丝中心的点画线连起来。

2、在平行螺旋弹簧线的视图上，各圈的轮廓线画成直线。

3、在图样上，当弹簧的旋向不作规定时，螺旋弹簧一律画成右旋，左旋弹簧也画成右旋，但要注明“左”字,M螺旋方向：有左右旋之分，常用右旋，图纸没注明的一般用右旋。⑿弹簧旋绕比：中径D与钢丝直径d之比。

?

1.4线径,扭簧转动1度多少扭矩

弹簧扭转的时候材料是拉伸或者剪切状态，因此这个可扭转的角度限制最后是因为材料的失效而造成的，当材料发生塑性变形时无法恢复原来状态。因此最后归结为材料的抗拉强度跟抗剪强度，当然用第四强度理论计算得到的Von Mises 应力为材料可承受的最大强度，结合弹簧的长度，便可以计算出最大允许扭转角度

要想设计扭簧，那么我们必须先了解扭簧参数以及工作中的一些技术要求。下面我们对照扭簧参数图来解释一下这些基本参数。

弹簧

d (弹簧线径) ：该参数描述了弹簧线的直径，也就是我们说的弹簧钢丝的粗细，默认单位mm。

Dd (心轴最大直径)：该参数描述的是工业应用中弹簧轴的最大直径，公差±2%。

D1 (内径)：弹簧的内径等于外径减去两倍的线径。扭簧在工作过程中，内径可以减小到心轴直径，内径公差±2%。

D (中径)：弹簧的中径等于外径减去一个线径。

D2 (外径) ：等于内径加上两倍的线径。扭簧在工作过程中，外径将变小，公差(±2%±0.1)mm。

L0 (自然长度)：注意：在工作过程中自然长度会减小，公差±2%。

Tum (扭转圈数)：弹簧绕制的圈数，圈数的不同直接影响扭簧的性能。扭簧的圈数越多扭力越小。

deg (原始角度)：扭簧的两个扭脚之间的原始角度。上图的原始角度为180°。

X1 (支承长度)：这是从弹簧圈身中轴到弹簧支承的长度，一般工作中是固定不动的，也就是我们所说的固定力臂，公差±2%。

X2 (施力长度)：这是从弹簧圈身中轴到弹簧施力点的长度，一般工作中是转动的，也就是我们所说的施力力臂，公差±2%。

A1 (工作扭转角度)：扭转弹簧的在工作中扭转的角度。

An (最大扭转角度)：扭转弹簧的最大扭转角度。

F1 (工作负荷)：扭簧在工作角度A1时作用在扭转弹簧支承上的作用力。

Fn (最大负荷)：允许作用在扭转弹簧支承上的最大力，对应的是An最大扭转角度时所需的作用力。

M1 (工作扭矩)：扭簧在工作角度A1时允许扭矩(牛顿*毫米)。

Mn (最大扭矩)：最大允许扭矩(牛顿*毫米)，对应的是An最大扭转角度时的允许扭矩。

K (弹簧刚度)：这个参数确定弹簧工作时的阻力。单位牛顿 * 毫米/度，公差±15%。

支承位置：扭转弹簧的支承有四个位置：0°, 90°,180°和 270°。

螺旋方向 ：右旋弹簧反时针方向旋，左旋弹簧顺时针方向旋。我们的所有弹簧两种旋向都可生产。

免责声明

本文来自腾讯新闻客户端创作者，不代表腾讯新闻的观点和立场。