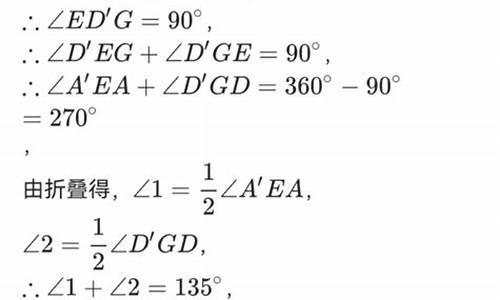扭转弹簧的载荷分析_扭转弹簧尺寸要求标准

1.弹簧设计的技术要求

2.弹簧的弹性系数和刚度是一个概念吗？常用单位是什么？

3.扭力弹簧有什么性能特点？

4.如图所示的两个弹簧，一个长一些、一个短些。

5.弹簧的弹性系数和哪些因素有关 请使用数据说明,

弹簧的弹性系数k与弹簧的直径，弹簧的线径，弹簧的材料，弹簧的有效圈数有关。具体关系是：

与弹簧圈的直径成反比，

与弹簧的线径的4次方成正比，

与弹簧的材料的弹性模量成正比，

与弹簧的有效圈数成反比.

c=F/λ＝Gd4/8D23＝Gd/8C3n

上式中：

c：弹簧的刚度，（即你所说的弹性系数，中学物理叫倔强系数k）；

F：弹簧所受的载荷；

λ：弹簧在受载荷F时所产生的变形量；

G：弹簧材料的切变模量；（钢为8×104MPa，青铜为4×104MPa）

d：弹簧丝直径；

D2：弹簧直径；

n：弹簧有效圈数；

C：弹簧的旋绕比（又称为弹簧指数 ）

由上式可知。当其它条件相同时，C值愈小的弹簧，刚度愈大，亦即弹簧愈硬；反之则愈软。还应注意到，C值愈小，弹簧内、外侧的应力差愈悬殊，卷制愈难，材料利用率也就愈低，并且在工作时将引起较大的扭应力。所以在设计弹簧时，一般规定C≥4，且当弹簧丝直径d越小时，C值越宜取大值。

其实上面这个公式是根据微段弹簧丝ds受转矩后扭转dθ，从而产生微量变形dλ，再将dλ积分而得到圆弹簧丝螺旋弹簧在受载荷F后所产生的变形量：

弹簧设计的技术要求

弹簧处理工艺

弹簧处理工艺

1 整定处理 Setting

又称“立定处理”。将热处理后的压缩弹簧压缩到工作极限载荷下的高度或压并高度（拉伸弹簧拉伸到工作极限载荷下的长度，扭转弹簧扭转到工作极限扭转角），一次或多次短暂压缩（拉伸、扭转）以达到稳定弹簧几何尺寸为主要目的的一种工艺方法。 2 加温整定处理 Hot-setting

又称“加温立定处理”。在高于弹簧工作温度条件下的立定处理。

3 强压处理 [Compressive] pre stressing

将压缩弹簧压缩至弹簧材料表层产生有益的与工作应力反向的残余应力，以达到提高弹簧承载能力和稳定几何尺寸的一种工艺方法。

4 加温强压处理 Hot-[compressive] prestressing

在高于弹簧工作条件下进行的强压处理

5 强拉处理 [tension] prestressing

将拉伸弹簧拉伸至弹簧材料表面产生有益的与工作应力反向的残余应力，以提高弹簧承载能力和稳定其几何尺寸的一种工艺方法。

6 加温强拉处理 Hot [tension] prestressing

在高于弹簧工作温度条件下进行的强拉处理

7 强扭处理 [torsion] prestressing

将扭转弹簧扭转至弹簧材料表层产生有益的与工作应力反向的残余应力，以提高弹簧承载能力和稳定其几何尺寸的一种工艺方法。

8 加温强扭处理 Hot [torsion]prestressing

高于弹簧工作温度条件下进行的强扭处理。

几种常见弹簧介绍

压缩弹簧(Compression Spring) 乃各圈分绕，因能承受压力，两端可为开式或闭式或绕平或磨平。下述为一压缩弹簧必要资料：

（1） 控制直径（Controlling diameter）（a）外径、（b）内径、（c）所套管之内径、（d）所穿圆杆之外径。

（2） 钢丝或钢杆之尺寸（Wire or bar size）。

（3） 材料（种类及等级）。

（4） 圈数：（a）总圈数及（b）右旋或左旋。

（5） 末端之形式（Style of ends）。

（6） 在某一挠区长度下之负荷。

（7） 一寸至几寸长度变化范围内之负荷比率。

（8） 最大体高“自由长”（Maximum solid height）。

（9） 运用时之最小压缩高。

压缩弹簧(Compression Spring)乃变体弹簧第一种，由直筒型、锥形至缩、凸腰形，乃至各种尾端之变体，均可依设计成型。

压缩弹簧(Compression Spring)为所有弹簧种类中最被广泛运用的一种，产品运用范围广及电子、电机、计算机、信息、汽机车、自行车、五金工具、礼品、玩具、乃至国防工业，因其设计与原理易于掌握，制造控制也最为单纯。

拉伸弹簧(Extension Spring)

乃各圈紧密围绕，以使其能受力而拉长，各端绕一环圈（Loop），下述为一拉伸弹簧之必要资料：

（1） 自由长度：（a）总长度、（b）全部圈长、（c）自钩圈内之长度。

（2） 控制直径：（a）外径、（b）内径、（c）所套管之内径。

（3） 钢丝尺寸“线径”。

（4） 材料（种类、等级）。

（5） 圈数：（a）总圈数及（b）右旋或左旋。

（6） 末端之形式。

（7） 钩内之负荷。

（8） 负荷率、挠曲度、每寸磅数。

（9） 最大拉伸长度。

拉伸弹簧（Extension Spring）乃典型之弹簧即弹簧之代表，由直筒形至各种变体，乃至挂钩之各种形状均能依设计成型。

拉伸弹簧（Extension Spring）为压缩弹簧之反向运用，运用范围大致较无具体产品类别，但操作控制较压缩弹簧高一级。

扭转弹簧(Torsion Spring)

各圈或是紧密围绕或是分开围绕，俾能适任扭转负荷（与弹簧轴线成直角）。弹簧之末端可绕成钩状或直扭转臂。下述为一扭转弹簧之必要资料：

（1） 自由长度。

（2） 控制直径：(a)外径、(b)内径、(c)所套管之内径，或(d)所穿越圆杆之外径。

（3） 钢丝尺寸“线径”。

（4） 材料（种类及等级）。

（5） 圈数：（a）总圈数及（b）右旋或左旋。

（6） 扭转力：偏转至某一角度之磅数。

（7） 最大挠度（自由位置算起之角度）。

（8） 末端之形式。

扭转弹簧（Torsion Spring）乃变体弹簧之极至，由单扭至双扭，乃至各种扭杆之变形，得依设计成型。

扭转弹簧（Torsion Spring）为所有弹簧类别中设计原理较为复杂的一种，型式的变化亦相当活泼，故设计时所涉及的理论也最为烦索。因此设计时亦较难掌握。

极细微弹簧

适用于精密电子组件。

此类弹簧线径在0.15mm~0.06mm之间,加上线径与各部尺寸均在1mm左右,故调试机具相当之难度与技术,一般运用范围为精密电子元器件或精密仪器、钟表等。

卷簧

可应用于卷尺、汽车起动马达、收纳线盒等。

卷簧又名（发条）其运用类似扭簧，但因其具有高扭力，与多角度之扭转力距故运用于长时间作功之机构，具有不易疲劳之特性。其运用类别大致可归类为卷尺、汽车起动马达、收纳线盒等。 弹片类

依材料之特性应用于不同环境之作动机构。

我们备用与车床不同原理之技术成型机，能克服冲床所难成型的料件。且相对具模具费低廉之优势，故广为客户接受。

勾环类

可依客户之设计应用在不同机构的固定或辅件

材质运用大致与弹簧类相一致，该类产品一般为客户依其需要作不同形状的设计，一般都作为辅件或机构件之固定。

弹簧的弹性系数和刚度是一个概念吗？常用单位是什么？

文档介绍：

弹簧的基本性能禾

设计要求

—低压电器十大工艺之一 弹簧的基本性能和设计要求

低压电器十大工艺

冷冲压

触头焊接

塑料成型

热处理

弹簧制造

电镀

线圈绕制

涂漆

铁芯制造

绝缘处理(浸漆) 弹簧的基本性能和设计要求

口弹簧的基本性能是在载荷作用下产生变形,卸载时释放能量恢复原形,

加载变形过程遵循一定的规律

口弹簧在低压电器中的作用:

A)保证动作力:如操作机构的作用力、触头压力、电磁系统的反作

用力等;

B)缓冲作用:由于电器上电磁铁的吸合、断开时有很大的冲击力,

用弹簧制成缓冲机构,可以吸收动能,减少冲击。

C)防止联结件松动:电器在工作中有振动,各联结部分需要用弹篑

的弹力压紧,防止松动。 弹簧的基本性能和设计要求

弹簧的特性线

载荷P(M)与变形F(φ)之间的关系曲线称为弹簧的特性线。弹簧

的特性线大致有三种类型:直线型、渐增型和渐减型

直线型——刚度不随载荷的变化而变化

渐增型——一刚度随载荷的増加而增大

渐减型——一刚度随载荷的增加而减小 弹簧的基本性能和设计要求

口常用弹簧的分类(按形状和结构分)

(1)圆柱螺旋弹簧

(2)变径螺旋弹簧

(3)蝶形弹簧

(4)平面蜗卷弹簧

(5)片弹篑 常用弹簧的分类

1)圆柱螺旋弹簧

这类弹簧多数由圆形截面材料制成,当同样空间条件下需要更大的刚度时

可选用矩形截面的材料。低压断路器中常用的圆柱型弹簧有以下三种

A)圆柱形螺旋压缩弹簧

这种弹簧结构简单,制造方便,特性接近于直线型,刚度值较稳定。

在低压断路器中常用作触头弹簧、螺旋管式电磁脱扣器的瞬时弹簧等。

B)圆柱形螺旋拉伸弹簧

性能和特点与压缩弹簧相同,主要承受拉伸载荷,其特性线是直线型,分

无初应力和有初应力两种。

在低压断路器中常用作机构主弹簧(一般有初应力)、拍合式电磁脱扣器

的瞬时弹簧和机构的复位弹簧等(一殷无初应力)

C)圆柱形螺旋扭转弹簧

这种弹簧主要承受扭

扭力弹簧有什么性能特点？

弹簧的弹性系数和刚度是一个概念。

弹簧的弹性系数是物体所受的应力与应变的比值。是载荷增量dF与变形增量dλ之比，即产生单位变形所需的载荷，弹簧的刚度计算公式为F'=dF/dλ。特性线为渐增型的弹簧，刚度随着载荷的增加而增大；而渐减型的弹簧，刚度随着载荷的增加而减少。

弹簧刚度是指使弹簧产生单位变形的载荷，用C和CT分别表示拉（压）弹簧的刚度与扭转弹簧的刚度。

扩展资料

在对一个因素发展变化预测的基础上，通过弹性系数对另一个因素的发展变化作出预测的一种间接预测方法。

弹性的概念被推广应用于社会经济领域。弹性系数被用来表示两个因素各自相对增长率之间的比率。在某一时期内能源消耗的增长率同工农业总产值的增长率的比率，就称为在该时期内能源消耗相对于工农业总产值的弹性系数。

弹性系数法在能源方面应用很广，常用的是能源需求相对于国民生产总值（GNP）的弹性系数。例如工业的弹性系数，中国1950～18年为0.95～1.0；美国1950～13年为0.94；日本1960～13年为1.0，15～18年降为0.43。大多数国家在1.0附近。

对于商品的市场需求量，可对消费者收入水平求弹性，称为需求量的收入弹性；对其价格求弹性，称为价格弹性；对另一产品（互补产品或代用产品）的价格求弹性，称为交互弹性。

百度百科—弹性系数

百度百科—弹簧刚度

如图所示的两个弹簧，一个长一些、一个短些。

扭力弹簧通过对材质柔软、韧度较大的弹性材料的扭曲或旋转进行蓄力，利用，使被发射物具有一定的机械能。现代的扭力弹簧扭力杆多用弹性极好的钢材制造，形式也有很大变化，有机械表里面的游丝，有玩具陀螺枪里的动力弹簧，也有坦克、汽车里的扭力杆。扭力杆体积小扭力大，作为交通运输工具的避震工具再好不过了。扭力弹簧是一款比较高精密的弹簧配件,生产扭力弹簧用普通的弹簧机不能满足1800度加工,一般生产扭力弹簧国内外都用万能弹簧机生产,精度比较高,万能弹簧机能实现不同角度不同形状的成型定位,是一款比较通用的电脑数控万能机,全自动生产设备万能弹簧机的主要功能弹簧机和电子行业中广泛使用的一种弹性元件，弹簧在受载时能产生较大的弹性变形，把机械功或动能转化为变形能，而卸载后弹簧的变形消失并回复原状，将变形能转化为机械功或动能。

弹簧的弹性系数和哪些因素有关 请使用数据说明,

(1)两个弹簧的关系

两个弹簧串联时，每个弹簧受力都是F，因此

F=k1x1

F=k2x2

F=K(x1+x2)=K(F/k1+F/k2)

解得：K=k1*k2/(k1+k2)

两个弹簧并联时，各受力为F/2，因此有

F/2=k1x1

F/2=k2x2

F=Kx=k1x1+k2x2

由于并联,x=x1=x2

所以 K=k1+k2

扩展资料：

串并联电路的电压规律是电路连接的一种理论知识，分为串联电路和并联电路，其中串联电路的总电压等于各部分电路两端电压之和，在并联电路中各支路用电器两端的电压相等，且等于总电压。

最直观的区别是这两种连接方式的电池所表现的不同特点，四节电池串联起来有6V，而并联则仍然只有1.5V。

1.串联电路：把元件逐个顺次连接起来组成的电路。如图，特点是：流过一个元件的电流同时也流过另一个。例如：节日里的小彩灯。 在串联电路中，闭合开关，两只灯泡同时发光，断开开关两只灯泡都熄灭，说明串联电路中的开关可以控制所有的用电器。

2.并联电路：把元件并列地连接起来组成的电路，如图，特点是：干路的电流在分支处分两部分，分别流过两个支路中的各个元件。

例如：家庭中各种用电器的连接。 在并联电路中，干路上的开关闭合，各支路上的开关闭合，灯泡才会发光，干路上的开关断开，各支路上的开关都闭合，灯泡不会发光，说明干路上的开关可以控制整个电路，支路上的开关只能控制本支路。

3.串联电路和并联电路的特点： 在串联电路中，由于电流的路径只有一条，所以，从电源正极流出的电流将依次逐个流过各个用电器，最后回到电源负极。

因此在串联电路中，如果有一个用电器损坏或某一处断开，整个电路将变成断路，电路就会无电流，所有用电器都将停止工作，所以在串联电路中，各几个用电器互相牵连，要么全工作，要么全部停止工作。 在并联电路中，从电源正极流出的电流在分支处要分为两路，每一路都有电流流过，因此即使某一支路断开，但另一支路仍会与干路构成通路。由此可见，在并联电路中，各个支路之间互不牵连。

串联分压，并联分流。

原理：在串联电路中，各电阻上的电流相等，各电阻两端的电压之和等于电路总电压。可知每个电阻上的电压小于电路总电压，故串联电阻分压。

在并联电路中，各电阻两端的电压相等，各电阻上的电流之和等于总电流（干路电流）。可知每个电阻上的电流小于总电流（干路电流），故并联电阻分流。 电阻的串并联就好像水流，串联只有一条道路，电阻越大，流的越慢，并联的支路越多，电流越大。

判断电路中用电器之间是串联还是并联。

串联和并联是电路连接两种最基本的形式，它们之间有一定的区别。要判断电路中各元件之间是串联还是并联，就必须抓住它们的基本特征，具体方法是：

（1）用电器连接法：分析电路中用电器的连接方法，逐个顺次连接的是串联；并列在电路两点之间的是并联。

（2）电流流向法：当电流从电源正极流出，依次流过每个元件的则是串联；当在某处分开流过两个支路，最后又合到一起，则表明该电路为并联。

（3）去除元件法：任意拿掉一个用电器，看其他用电器是否正常工作，如果所有用电器都被拿掉过，而且其他用电器都可以继续工作，那么这几个用电器的连接关系是并联；否则为串联。

最直观的区别是这两种连接方式的电池所表现的不同特点，四节电池串联起来有6V，而并联则仍然只有1.5V。

1.串联电路：把元件逐个顺次连接起来组成的电路。如图，特点是：流过一个元件的电流同时也流过另一个。例如：节日里的小彩灯。 在串联电路中，闭合开关，两只灯泡同时发光，断开开关两只灯泡都熄灭，说明串联电路中的开关可以控制所有的用电器。

2.并联电路：把元件并列地连接起来组成的电路，如图，特点是：干路的电流在分支处分两部分，分别流过两个支路中的各个元件。例如：家庭中各种用电器的连接。 在并联电路中，干路上的开关闭合，各支路上的开关闭合，灯泡才会发光，干路上的开关断开，各支路上的开关都闭合，灯泡不会发光，说明干路上的开关可以控制整个电路，支路上的开关只能控制本支路。

3.串联电路和并联电路的特点： 在串联电路中，由于电流的路径只有一条，所以，从电源正极流出的电流将依次逐个流过各个用电器，最后回到电源负极。因此在串联电路中，如果有一个用电器损坏或某一处断开，整个电路将变成断路，电路就会无电流，所有用电器都将停止工作。

所以在串联电路中，各几个用电器互相牵连，要么全工作，要么全部停止工作。 在并联电路中，从电源正极流出的电流在分支处要分为两路，每一路都有电流流过，因此即使某一支路断开，但另一支路仍会与干路构成通路。由此可见，在并联电路中，各个支路之间互不牵连。

弹簧行业在整个制造业当中虽然是一个小行业，但其所起到的作用是绝对不可低估的。国家的工业制造业、汽车工业要加快发展，而作为基础件、零部件之一的弹簧行业就更加需要有一个发展的超前期，才能适应国家整个工业的快速发展。

另外，弹簧产品规模品种的扩大、质量水平的提高也是机械设备更新换代的需要和配套主机性能提高的需要，因此，整个国家工业的发展，弹簧产品是起到重要作用的。日用品业及五金业，包括打火机、玩具、锁具、门铰链、健身器、床垫、沙发等等，就数量而言，对弹簧需求量最大，数以百亿件，技术要求不高，价格非常低，一般由分散在全国各地的小弹簧厂生产，它们在成本上有独特的优势，大弹簧厂难以和他们竞争。

因而也不时引发新弹簧企业诞生，在未来，市场需求会以每年7%~10%的速度增长。中国加入WTO之后，日用五金产品出口量明显增长，弹簧需求随之拉动，但受到国际市场需求量、贸易壁垒的影响，国际市场有其不确定的一面。

弹簧可以分为以下6类：

1、扭转弹簧，是承受扭转变形的弹簧，它的工作部分也是密绕成螺旋形。扭转弹簧端部结构是加工成各种形状的扭臂，而不是勾环。扭力弹簧利用杠杆原理，通过对材质柔软、韧度较大的弹性材料扭曲或旋转，使之具有极大的机械能。

2、拉伸弹簧是承受轴向拉力的螺旋弹簧。在不承受负荷时，拉伸弹簧的圈与圈之间一般都是并紧的没有间隙。

3、压缩弹簧是承受轴向压力的螺旋弹簧，它所用的材料截面多为圆形，也有用矩形和多股钢萦卷制的，弹簧一般为等节距的，压缩弹簧的形状有：圆柱形、圆锥形、中凸形和中凹形和少量的非圆形等，压缩弹簧的圈与圈之间会有一定的间隙，当受到外载荷的时候弹簧收缩变形，储存变形能。

4、渐进型弹簧，这种弹簧用了粗细、疏密不一致的设计，好处是在受压不大时可以通过弹性系数较低的部分吸收路面的起伏，保证乘坐舒适感，当压力增大到一定程度后较粗部分的弹簧起到支撑车身的作用，而这种弹簧的缺点是操控感受不直接，精确度较差。

5、线性弹簧，线性弹簧从上至下的粗细、疏密不变，弹性系数为固定值。这种设计的弹簧可以使车辆获得更加稳定和线性的动态反应，有利于驾驶者更好的控制车辆，多用于性能取向的改装车与竞技性车辆，坏处当然是舒适性受到影响。

6、短弹簧短弹簧相比原厂弹簧要短一些，

参考资料：

弹簧的弹性系数k与弹簧的直径,弹簧的线径,弹簧的材料,弹簧的有效圈数有关.具体关系是：

与弹簧圈的直径成反比,

与弹簧的线径的4次方成正比,

与弹簧的材料的弹性模量成正比,

与弹簧的有效圈数成反比.

c=F/λ＝Gd4/8D23＝Gd/8C3n

上式中：

c：弹簧的刚度,（即你所说的弹性系数,中学物理叫倔强系数k）；

F：弹簧所受的载荷；

λ：弹簧在受载荷F时所产生的变形量；

G：弹簧材料的切变模量；（钢为8×104MPa,青铜为4×104MPa）

d：弹簧丝直径；

D2：弹簧直径；

n：弹簧有效圈数；

C：弹簧的旋绕比（又称为弹簧指数 ）

由上式可知.当其它条件相同时,C值愈小的弹簧,刚度愈大,亦即弹簧愈硬；反之则愈软.还应注意到,C值愈小,弹簧内、外侧的应力差愈悬殊,卷制愈难,材料利用率也就愈低,并且在工作时将引起较大的扭应力.所以在设计弹簧时,一般规定C≥4,且当弹簧丝直径d越小时,C值越宜取大值.

其实上面这个公式是根据微段弹簧丝ds受转矩后扭转dθ,从而产生微量变形dλ,再将dλ积分而得到圆弹簧丝螺旋弹簧在受载荷F后所产生的变形量：